Current projects
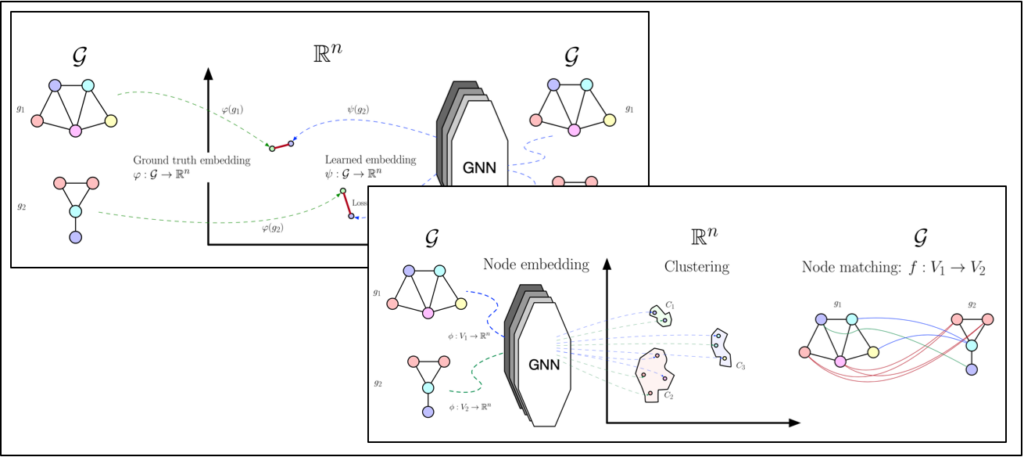
Neural Networks for Learning Graph Embedding and Graph Matching (2024 — 2028)
Abstract: The proposed project is concerned with graph-based pattern recognition. Research in this area can be roughly divided into three time periods, viz. the eras of graph matching, graph kernels, and graph neural networks. The overall objective of the present project is to develop and research robust methods which combine the best ideas and methods that emerged from these three eras. This way, we aim to introduce novel graph-based methods that significantly exceed the current state of the art, both in terms of speed and accuracy. Read More…
Exploring Research Opportunities for Automatic Text Document Summarization (2023 — 2024)
Abstract: The proposed project serves as a preparatory project to lay the groundwork for a large-scale research project possibly funded by the Swiss National Science Foundation (SNSF). We use the following terminology in the present document: The terms ”present application” and ”preparatory project” refer to the requested ”Hasler Foundation Grant”, while ”principal application” and ”principal project” refer to the actual application and project that will potentially be financed via SNSF. Read More…
Novel Paradigms for Machine Learning in Medicine (2023 — 2024)
Abstract: The overarching goal of the planned project1 is to research novel state-of-the-art algorithms in digital medicine using techniques from artificial intelligence and machine learning. In particular, we plan to develop algorithmic solutions and computational frameworks that can help practitioners analyze medical data from multiple sources to identify diseases, decide on the next step of treatment, determine potential problems, and improve the overall efficiency of care. Read More…
A PROSE – Advanced PROofreading SErvices (2022 — 2026)
Abstract: Many proof-reading services are currently focused on orthography, grammar, punctuation, and typography. In these areas, unresolved challenges for automated proofreading exist, comprising detection of so-called real-word errors, compliance with specific typesetting rules and company-specific spelling guidelines, and ensuring the use of gender-neutral language. Further tasks that currently require better solutions are the automatic detection of subjective language and incorrect information (e.g. dates, addresses) in customer documents. Read More…
Spatio-temporal graph convolutional networks – a novel deep learning approach to forecasting river temperatures (2022 — 2026)
Abstract: The Federal Office for the Environment (FOEN) analyses several environmental aspects of Switzerland. The monitoring of water temperatures over long time periods belongs to one of the most important tasks of the Hydrology Division of FOEN. At the moment, the Hydrology Division maintains approximately 80 metering stations. Stations measure various parameters such as water temperature, discharge, water level etc. Read More…
Past Projects
- Novel State-of-the-Art Graph Matching Algorithms
- Knowledge via Graph Reasoning
- 14 Weeks of Java – A Novel Approach for Teaching Java
- Graph Based Signature Verification
- User Authentication based on Freehand Sketches
- Graph Based Keyword Spotting in Handwritten Historical Documents
- Reducing the Overestimation of Graph Edit Distance Approximation
- Improving Graph Edit Distance
- Development of a Graph Matching Toolkit